Kartenkunde
Karten waren und sind schon immer eine wichtige Navigationshilfe gewesen. Dabei geht es immer um die Fragen, wo bin ich und in welche Richtung muss ich gehen, um zu meinem Zielort zu kommen. Damit stellen sich folgende Anforderungen: Die Position eines Ortes auf der Erde muss eindeutig angegeben werden können und es muss ein Kurs, also eine Richtung, zu definieren sein.
Einen Punkt eindeutig zu finden wurde mittels des geografischen Koordinatensystems ermöglicht. Einen Kurs an einer Kugel abzugreifen ist aber etwas schwierig, also benötigt man eine flache Darstellung der fast runden Erdkugel. Auf der flachen Abbildung ist der Kurs aber nur eine Gerade und es fehlt ihm der Radius der Erdkrümmung. Das führt zu Problemen mit dem Winkel und der Länge.
Die Probleme, welche gelöst werden mussten, sind also die flache Abbildung der Koordinaten eines Ortes und die Möglichkeit einen Kurs finden zu können, möglichst winkel- und längentreu, auf einer flachen Ebene. Diese Anforderungen, die Abbildung der gekrümmten Erdoberfläche auf einer ebenen Karte sowie die Orts- und Kursbestimmung dort, wurden mittels der Kartennetzentwürfe und Gittersysteme gelöst.
Das geografische Koordinatensystem der Erde
Um einen beliebigen Punkt auf einer Fläche zu definieren benötigt man Koordinaten, in diesem Fall zwei (X- und Y-Achse). Um diese Koordinaten zu erhalten, ist die Erde mit einem geografischen Koordinatensystem, die Breiten- und Längengrade, versehen worden, die quasi die X- und Y-Achsen bilden. Die Koordinaten werden in Grad, Minuten und Sekunden angegeben. Es sind Winkelmaße, da die Erde eine nahezu runde Form hat. Folgende Darstellungen sind üblich:
- Grad Minuten Sekunden (46° 32' 30"N)
- Grad Dezimalminuten (46° 32,500'N)
- Dezimalgrad: (46,5410°N)
Umrechnung
| von ↓ / nach → | Grad Minuten Sekunden 46° 32' 30"N |
Grad Dezimalminuten 46° 32,500'N |
Dezimalgrad 46,541°N |
|---|---|---|---|
| Grad Minuten Sekunden 46° 32' 30"N |
Minuten + Sekunden : 60 32' + 30" : 60 = 32,500' Dez |
Grad + Minuten : 60" 46° + 32,5': 60" = 46,541° Dez | |
| Grad Dezimalminuten 46° 32,500'N |
Minuten und Dezimalstellen x 60 46° 32' und 0,5' x 60 = 46° 32' 30" |
Grad + Dezimalminuten : 60" 46° + 32,5' : 60" = 46,541° | |
| Dezimalgrad 46,541°N |
Dezimalstellen x 60 = Dezimalminuten, Dezimalstellen x 60 46° und 0,541' x 60 = 46° 32,5' Die halbe Sekunde der Dezimalminuten 0,5" x 60 = 30" 46° 32' 30" |
Dezimalstellen x 60 = Dezimalminuten 46° 0,541' x 60 = 46° 32,5' |
Breitengrade
Die Breitengrade (auch LAT von Latitude) verlaufen parallel zum Äquator und heissen daher auch Parallelkreise. Der Äquator ist ebenfalls ein Breitengrad, mit der Gradzahl 0°. Alle Breitengrade, die sich nördlich von ihm befinden erhalten den Zusatz N, alle die südlich liegen S. Die Gradzahl gibt den Winkel vom Äquator zum gewählten Breitengrad mit der Erdmitte als Scheitelpunkt an und reicht von 0° bis 90° am Nord- bzw. Südpol. Der Abstand der Breitengrade ist, bis auf die Polkreise, immer gleich und beträgt ca. 111 km. Dafür nimmt der Umfang der Breitengrade zu den Erdpolen hin ab. Der größte Breitengrad ist der Äquator mit einem Umfang von ca. 40.000 km.
Längengrade
Die Längengeraden (auch LONG von Longitude) verlaufen senkrecht um die Erde und laufen durch beide geografischen Pole. Alle Längengerade sind gleich lang, ihr Abstand zueinander nimmt aber zu den Erdpolen hin ab. Ein halber Längengrad (von Pol zu Pol) ist ein Meridian. Je nach System gibt es eine unterschiedliche Anzahl von Längengraden. Mit am gebräuchlichsten ist die Einteilung in 180 Längengrade (oder 360 Meridiane). Sie stehen im Rechten Winkel (90°) zu den Breitengraden, was sehr wichtig für die Kursberechnung ist. Per Definition verläuft der erste Meridian (Nullmeridian, 0°) durch die alte Sternwarte von Greenwich, England. Ihm gegenüber, also bei 180° verläuft die Datumsgrenze. Auch hier wird ein Winkelmaß angegeben, in dem Fall der Winkel vom Nullmeridian zum gewünschten Meridian, mit der Erdmitte als Scheitelpunkt und von 0° bis 180°, jeweils nach Osten oder Westen. Alle Längengrade östlich vom Nullmeridian haben den Zusatz E (E für East = Ost), alle die westlich liegen W.
Positionsangaben
Eine Position wird nun eindeutig durch die Angabe des Breiten- und Längengrades bestimmt. So hat die Winchrampe in Fürstenau die geografischen Koordinaten :
- 52° 32' 16"N 7° 38' 14"E oder
- 52° 32,273'N 7° 38,226'E
Ist Nord gleich Nord?
Nein. Es gibt verschiedene Nordangaben. Da gibt es den magnetischen Nordpol, der jedoch seine Position ständig verändert. Daher ist er schlecht als Bezugspunkt für Karten geeignet.
Der geografische Nordpunkt wird auch als rechtweisend Nord bezeichnet. Dies ist der Nordpunkt, der sich nicht verändert. Der bekannte Nord- oder Polarstern markiert diesen. Durch ihn verlaufen auch die Längengrade, daher auch Meridian-Nord. Navigiert man mit dem Kompass, muss man u.U. die Differenz, die Deklination, zwischen den örtlichen Magnetverhältnissen und dem geografischen Nordpol kennen. Sie ist je nach Ort an dem man sich befindet unterschiedlich. Derzeit beträgt die Abweichung in Mitteleuropa 1,5° Ost. Zur sicheren Navigation müssen Abweichungen ab 5° berücksichtigt werden. Hier kann die aktuelle Deklination angezeigt werden.
Dann gibt es noch das Kartennord oder auch Gitternord. Nach Nord ausgerichtete Linien auf Karten beziehen sich auf diesen Punkt. Mit einer Ausnahme! Der Hauptmeridian bei verschiedenen Kartennetzentwürfen (Gauß-Krüger, UTM) fällt mit rechtweisend Nord zusammen. Alle anderen senkrechten Gitterlinien nicht. Die Abweichung zwischen rechtweisend Nord und den Gitterlinien nennt man Meridiankonvergenz.
Von der Kugel zur Karte
Um nun dieses, eine Kugel umfassende Koordinatensystem, auf eine flache Karte abzubilden, bedarf es einiger Kompromisse. Würde man das Koordinatensystem 1:1 auf eine flache Karte übertragen, käme es zwangsläufig zu Verzerrungen. Bedenkt man z.B. den kleiner werdenden Abstand der Längengrade zueinander. Würde man diese Verjüngung auf eine Karte übernehmen, ginge der für die Navigation so wichtige rechte Winkel verloren. Belässt man ihn, wird die Fläche verzerrt. Daher ist eine Karte immer für einen Zweck optimiert. Sie ist entweder hauptsächlich:
- flächentreu
- Die abgebildetet Fläche entspricht der Realität, z.B. bei geologischen Karten.
- winkeltreu
- Die Winkel in der Karte entsprechen der Realität, z.B. bei topografischen Wanderkarten
- streckentreu
- Eine 100%tige Längentreue ist nicht möglich, aber für unsere Zwecke ausreichend. Die abgebildeten Abstände auf der Karte entsprechen also fast der Realität, z.B. bei Autokarten
Eine Karte kann nie allen drei Anforderungen gerecht werden. Für Offroadnavigation sowie Navigation im Allgemeinen sind winkeltreue Karten am besten geeignet.
Und als wäre das nicht schon schwierig genug, kommt hinzu, dass die Erde gar nicht wirklich rund ist, sondern sie ist ein Ellipsoid, d.h. sie ist an den Erdpolen etwas abgeflacht und am Äquator etwas breiter. Dies macht die Übertragung auf eine flache, zweidimensionale Karte noch schwieriger. Es gibt verschiedene Definitionen des Ellipsoids mit jeweils unterschiedlichen Parametern die diese Unförmigkeit beschreiben: Das geodätische Datum.
Die Kartengitter
Auf einer Karte können ein oder mehrere Gitter eingezeichnet bzw. am Rand angedeutet sein. Normalerweise findet sich das geografische Gitter (Koordinatensystem) am Rand angedeutet, während ein rechtwinkliges Gitter eingezeichnet ist. Dieses Gitter dient zur Positions- und Kursbestimmung mittels eines Kompass und basiert auf einem Kartennetzentwurf.
Wichtige Angaben auf der Karte
Zur Vergrößerung bitte auf die Karte klicken und dann im Browser einen größeren Zoomlevel einstellen.
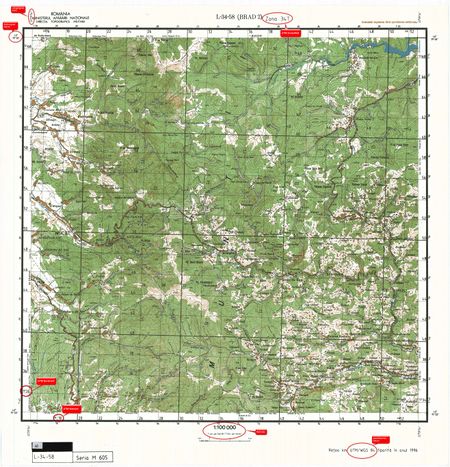
Um mit Karten vernünftig arbeiten zu können oder um Positionsangaben auszutauschen, müssen die Rahmenparameter der Karte bekannt und auf ihr angegeben sein. Nicht alle Angaben bzw. Koordinatensysteme finden sich auf allen Karten. Wichtige Informationen wären:
- Geodätisches Datum
- Beispielkarte: WGS84
- Dieses Datum ist z.B. wichtig um Koordinaten korrekt zwischen einem GPS Gerät und der Karte umrechnen zu können. Im GPS Gerät muss das gleiche Datum eingestellt sein. In Notfällen ist dieses Datum zusammen mit dem Gitternetzentwurf anzugeben.
- Kartennetzentwurf
- Beispielkarte: UTM
- Diese Information gibt an, wie Koordinatenangaben an der Seite zu interpretieren sind und wie eine Positionsangabe zu erfolgen hat.
- Maßstab
- Beispielkarte: 1:100.000
- Der Maßstab gibt an, wie Entfernungen auf der Karte in die Realität umzurechnen sind und umgekehrt. Hier ist 1 cm Karte = 1 km (100.000 cm) in der Realität.
- Geografische Koordinaten
- Der Breiten- und Längengrad
Abhängig vom Kartennetzentwurf:
- UTM Zonenfeld
- Beispielkarte: 34T
- Das Zonenfeld grenzt den abgebildeten Bereich auf ein Region ein und bestimmt den Hauptmeridian.
- UTM Ost- und Nordwert.
- Die Koordinatenwerte für das UTM Gitternetz.
Geodätisches Datum
Das Geodätische Datum gibt die verschiedenen Parameter des Erd-Ellipsoids an, der von einem Kartennetzentwurf verwendet wird. Es werden verschiedene Ellipsoide als Grundlage verwendet. Zwei weit verbreitete sind:
- WGS84 (ETRS89)
- WGS = World Geodetic System
- Dieses Datum wird im Wesentlichen in Europa verwendet.
- Es definiert als Radius zum geografischen Nordpol 6.356,752 km und zum Äquator 6.378,137 km.
- International
- Hier werden als Radien 6.356,912 km und 6.378,388 km definiert.
Bei GPS basierten Navigationsgeräten kann man dieses Datum einstellen. Es ist wichtig für die korrekte Umrechnung zwischen GPS/geografischen Koordinaten und dem Kartennetzentwurf der Karte.
Kartennetzentwurf
Manchmal auch Gitternetzentwurf genannt. Die Übertragung eines Koordinatensystems von dem Ellipsoid auf eine flache Karte wird mittels eines Kartennetzentwurfs bewerkstelligt, von denen es mehrere gibt. Diese Entwürfe berücksichtigen dabei die unterschiedlichen Angaben zu der Erdform mittels des geodätischen Datums. Eine ordentliche Karte gibt den verwendeten Entwurf als auch das geodätische Datum an. Sehr weit verbreitet als Basis für viele andere Kartennetzentwürfe ist die normale Mercator-Projektion. Ihr Nachteil ist die starke Krümmung/verzerrung zu den Randbereichen hin. Daher gibt es verbesserte Entwürfe, die auf der Mercator-Projektion basieren. Die bekanntesten Vertreter sind das Gauß-Krüger Netz und UTM (Universale transversale Mercator, siehe Mercator).
Gauß-Krüger Gitter
Dieser Entwurf wird auch als Transversale Mercatorprojektion oder German Grid bezeichnet. Es war lange die Grundlage deutscher Karten, die aber schon seit einigen Jahren auf UTM umgestellt wurden. Bei der diesem Entwurf zugrunde liegenden normalen Mercator-Projektion treten zu den Rändern starke Verzerrungen auf. Daher verwendet dieses Gitter mehrere Projektionen, um so die Verzerrungen in einem unbedeutendem Rahmen zu halten.
In diesem System wird die Erde in 3° breite senkrechte Streifen, die Hauptmeridiane, unterteilt. Diese laufen in Deckung zu dem dazugehörigen Meridian des geografischen Systems und zeigen nach rechtweisend Nord. Da alle anderen senkrechten Gitterlinien des Netzes parallel zu dem Hauptmeridian verlaufen, zeigt nur der Hauptmeridian nach rechtweisend Nord. Sie werden von 0° bis 357° in östlicher Richung durchgezählt und erhalten eine Kennziffer:
- Hauptmeridian° : 3 = Kennziffer.
So hat der Hauptmeridian, der für Deutschland wichtig ist, die Kennziffer 2 (6° : 3 = 2).
Gauß-Krüger verwendet in Deutschland den Bessel-Ellipsoid als geodätisches Datum. Bei der Nutzung dieses Systems muss beachtet werden, dass es viele nationale Abwandlungen gibt.
Positionsbestimmung
Rechtswert
Der Rechtswert gibt den Abstand zum Hauptmeridian des Kartenabschnitts in Metern wieder. Der Hauptmeridian hat immer einen Wert von 500, um negative Vorzeichen auszuschliessen. Eine Angabe am Kartengitter von 3449 besagt
- der Hauptmeridian ist 9°
- Die erste Zahl mit 3 multiplizieren um den Hauptmeridian zu bestimmen: 3 x 3° = 9°.
- dass die Gitternetzlinie 51 km westlich von Hauptmeridian liegt
- Die letzten drei Ziffern 449 sind kleiner als 500 (Hauptmeridian) und das bedeutet er liegt westlich
- 500 - 449 = 51
3551 würde bedeuten
- der Hauptmeridian ist 3 x 3° = 9°
- dass die Linie 51 km östlich vom Hauptmeridian liegt
- 551 ist größer 500 und das bedeutet er liegt östlich:
- 551 - 500 = 51
Hochwert
Für nördlich liegende Positionen hat der Äquator den Wert 0. 5629 sind demnach 5.629 km nördlich des Äquators.
Für südliche Punkte gibt es nicht wirklich Angaben, da dieses System ein deutsches ist und eher national angelegt war. Mir ist keine südliche Angabe bekannt.
Die Meterzahlen innerhalb des Gitterfeldes müssen messtechnisch mit einem Lineal ermittelt werden. In einer Karte mit dem Maßstab 1:100.000 entsprächen 5 mm = 500 m in der Realität.
Eine Position wird wie folgt angegeben: 3449500 5629250 und entspräche der Kartenposition in einem 1:100.000 Maßstab von
- Von der senkrechten Gitternetzlinie 3449 5 mm nach rechts
- Von der waagerechten Gitternetzlinie 5629 2,5 mm nach oben
- Dort wo sich die Linien kreuzen ist die gesuchte Position.
UTM
Bei der UTM zugrunde liegenden Mercator-Projektion, wird die Erde in 60 jeweils 6° breite senkrechte Streifen (6°x60=360°) und von 84° Nord bis 80° Süd durch jeweils 8° (8 Breitegrade, ca. 888 km) hohe Streifen in Zonen aufgeteilt. Die Verzerrungen sind geringer und liegen in den Randbereichen der Zonen. Es wird vom 180° Meridian (Datumsgrenze) ostwärts mit Zone 1 angefangen zu zählen. In Nordrichtung wird vom 80°S bis zum 84°N in mit den Buchstaben von C bis X gezählt, wobei die Buchstaben I und O nicht verwendet werden. Jede Zone hat einen Hauptmeridian, der von der linken und rechten Zonengrenze jeweils 3° entfernt liegt. Zone 1 geht also von 180°W bis 174°W und der Hauptmeridian ist 177°W. Nur der Hauptmeridian ist nach rechtweisend Nord ausgerichtet. Da alle senkrechten Gitterlinien parallel zum Mittelmeridian verlaufen, weichen diese von rechtweisend Nord ab. Diese Abweichung nennt sich Meridiankonvergenz. Die UTM Projektion hält bei Winkeltreue die Verzerrung an den Rändern (vom Hauptmeridian entfernte Gebiete) vernachlässigbaren Grenzen.
Die Hauptmeridiane für deutsches und mitteleuropäisches Gebiet sind der 6.E, 9.E, 12.E und 15.E. Deutschland liegt hauptsächlich im Zonenfeld 32U.
UTM deckt die gesamte Erde mit Ausnahme der Pole ab. Für die Pole gibt es eigene Projektionen, die sich Universal Polar Stereographic (UPS) nennen.
Auf UTM Karten wird das Zonenfeld angegeben. Der Hauptmeridian errechnet sich dann durch eine einfache Formel, hier für die Zone 32U gezeigt: Differenz von Zone 32 zu Zone 1 = 31 Zonen (32 - 1 = 31). Das entspricht einem Längenunterschied in Grad von 31 x 6° = 186°. Der Hauptmeridian für 32U ist die Differenz vom Hauptmeridian von Zone 1 und dem Längenunterschied der Zone: 177° - 186° = -9° = 9°E. Negative Werte liegen östlich des Nullmeridians, positive liegen westlich.
Der Hauptmeridian einer Zone ist 177° - ((Zonnenummer-1) x 6).
UTM verwendet mittlerweile WGS84 als Kartendatum. Früher kam auch das Hayford Modell zum Einsatz.
Positionsbestimmung
Was im Gauss-Krüger Gitter der Rechts- und Hochwert ist, ist hier der Ost- und Nordwert.
Ostwert
Der Ostwert gibt den Abstand zum Hauptmeridian der Zone in Metern wieder. Der Hauptmeridian hat immer einen Wert von 500.000 m, um negative Vorzeichen westlich des Hauptmeridians auszuschliessen. Die Koordinatenangaben sind immer sechsstellig. Eine Angabe von 449000 besagt
- dass die Gitternetzlinie 51.000 m (51 km) westlich von Hauptmeridian liegt
- 449000 ist kleiner als 500000 und das bedeutet er liegt westlich
- 500.000 m - 449.000 m = 51.000 m
551000 würde bedeuten
- dass die Linie ist 51.000 m (51 km) östlich vom Hauptmeridian liegt
- 551.000 ist größer 500.000 und bedeutet er liegt östlich
- 551.000 m - 500.000 m = 51.000 m
Nordwert
Für nördlich liegende Positionen hat der Äquator den Wert 0. Ein Nordwert von 5629000 liegt demnach 5.629 km (5.629.000 m) nördlich des Äquators.
Für südliche Punkte hat der Äquator den Wert von 10.000.000 m. Ein Punkt mit 5629000 liegt demnach
- 10.000.000 m - 5.629.000 m = 4.371 km südlich des Äquators. Ob ein Punkt nördlich oder südlich des Äquators liegt ist dem hinten an gestellten N bzw. S oder dem Zonenfeld zu entnehmen.
Beispiel mit Karte
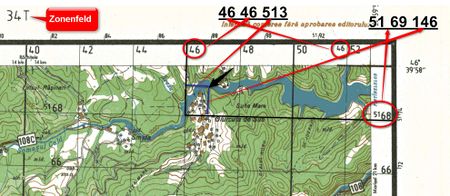
Der in der Karte markierte Punkt (schwarzer Pfeil) hat folgende Koordinaten: UTM 34T 646513E 5169146N. Zerlegt bedeutet dies:
- UTM Gitter, Zonenfeld 34T
- Nach obiger Formel berechnet ist 21°E der Hauptmeridian für 34T (177° - ((34 - 1) x 6) = -21°).
- Nach Norden gesehen liegt der Ort grob zwischen 4.440 km und 5.288 km nördlich des Äquators (Zonenfeld T).
- Der Ostwert
- Die Zahl 4646 kann vom Kartenrand ermittelt.
- Die erste Zahl 4 steht bei dieser Karte für die östliche Zonengrenze vom Nullmeridian aus gesehen (4 x 6° = 24°). Aus dieser kann auch der Hauptmeridian ermittelt werden: 4 x 6° - 3° = 21°.
- Die folgenden drei Stellen 646 geben den Ostwert dieser Linie an. Diese Linie liegt 146.000 m (146 km) vom Hauptmeridian entfernt:
- 646.000 m - 500.000 m = 146.000 m
- Die 513 Meter sind unter Beachtung des Maßstabs aus der Karte heraus von der betreffenden Gitternetzlinie (46) zu messen:
- Die Karte hat den Maßstab 1:100.000, d.h. 1 cm Karte entspricht 1 km in der Realität. Der Punkt ist ca. 5 mm von der senkrechten Gitternetzlinie 4646 entfernt.
- Demnach liegt er also 146,531 km östlich vom Hauptmeridian 21°.
- Der Nordwert
- Die Zahl 5168 kann vom Kartenrand ermittelt werden und zerlegt sich wie folgt:
- Die Gitterlinie ist 5.168.000 m (5.168 km) nördlich vom Äquator entfernt.
- Auf der Karte messen wir 11,46 mm von der 5168 Linie zum gesuchten Punkt.
- Die Karte hat den Maßstab 1:100.000, d.h. 1 cm Karte entspricht 1 km in der Realität. Somit liegt der Punkt schon auf der 5169 Line, da in der Karte ein Feld 2 km hoch ist.
- Demnach ist der Punkt ca. 146 m von der (nicht eingezeichneten) Gitternetzlinie 5169 entfernt oder 1,146 km von der eingezeichneten 5168 Linie.
Koordinaten umrechnen
Werden Koordinaten unterschiedlichem Ursprungs ausgetauscht, müssen diese umgerechnet werden. Hier wird erklärt, wie man geografische Koordinaten mit Karten austauscht.
Geografische Koordinaten (GPS) / Karte mit geografischem Gitter
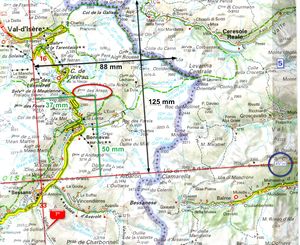
Wir verwenden zur Erklärung den Punkt Pointe des Arses (rot umrandet).
Umrechung
Zuerst ermittelt man die Aufteilung des Gitters. Bei der Beispielkarte ist jedes Gitterfeld 10' hoch und breit. Diese Werte kann man am Kartenrand ablesen (blau umrandet), es ist die Differenz zwischen zwei benachbarten Kartennetzlinien. Nun sucht man sich den Schnittpunkt des relevanten Gitters von dem gewünschten Punkte heraus. Beginnend vom gewünschten Punkt auf der Karte in Richtung 0° gehen. Hier also zuerst in Richtung Süd und wir kommen zur Linie 45° 20'N und dann Richtung West und kommen zur Linie 7°E. Das relevante Gitter hat also den Ursprung im linken, unteren Schnittpunkt bei 45° 20,00'N 7° 00,000'E. Nun messen wir wie hoch und wie breit das Gitterfeld ist. Je größer der Maßstab, je wichtiger ist es, genau auszumessen. Bei der Beispielkarte kommen wir auf 125 mm x 88 mm. D.h. 10' Breite entsprechen 125 mm und 10' Länge entsprechen 88 mm.
Jetzt wird der Breitengrad des gewünschten Punktes ausgemessen. Von der Gitterlinie 45° 20'N messen wir die Distanz hoch bis zum Pointe des Arses und entnehmen dem Lineal 50 mm. Dann der Längengrad von der Gitterline 7°E nach rechts, hier haben wir 37 mm.
Zum ermitteln der Dezimalminuten nutzen wir den Dreisatz und setzen die Werte ein:
- Gemessene Distanz x Gittergröße in Min. : Gittergröße in mm
- 50 mm x 10' : 125 mm = 4,000'
- 37 mm x 10' : 88 mm = 4,200'
Diese Werte addieren wir nun zu dem Schnittpunkt unseres Gitters. Damit ergeben sich die geografischen Koordinaten des Pointe des Arses:
- 45° 24,000'N 7° 04,200'E
Geografische Koordinaten (GPS) / Karte mit geodätischem Gitter
Literatur
- Wolfgang Linke: Orientierung mit Karte, Kompass, GPS. Delius Klasing, 978-3-76883314-1